1. Khái niệm về “Giải quyết một số vấn đề”

Giải quyết vấn đề là gì?

• Để giải quyết vấn đề:
  1. Phát biểu chính xác bài toán
     • Hiện trạng ban đầu,
     • Kết quả mong muốn,..
  2. Phân tích bài toán.
  3. Thu thập và biểu diễn dữ liệu, tri thức cần thiết để giải bài toán.
  4. Lựa chọn kỹ thuật giải quyết thích hợp.

2. Không gian trạng thái - Mở đầu

Khi biểu diễn một vấn đề như là một đồ thị không gian trạng thái, chúng ta có thể sử dụng lý thuyết đồ thị để phân tích cấu trúc và độ phức tạp của các vấn đề cũng như các thủ tục tìm kiếm.

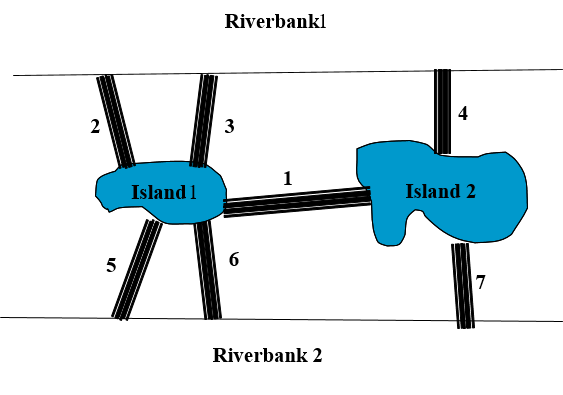
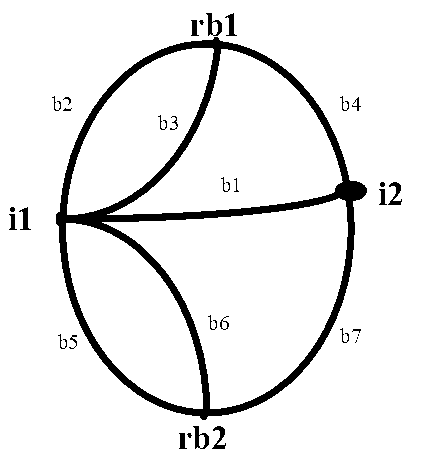
Hệ thống cầu thành phố Konigsberg và biểu diễn đồ thị tương ứng (Leonhard Euler)

Khái niệm về Không gian trạng thái

Một KGTT (state space) là 1 bộ [N, A, S, GD] trong đó:

• N (node) là các nút hay các trạng thái của đồ thị.
• A (arc) là tập các cung (hay các liên kết) giữa các nút.
• S (start) là một tập chứa các trạng thái ban đầu của bài toán.(S Ì N Ù S ¹ Æ)
• GD (Goal Description) chứa các trạng thái đích của bài toán (GD Ì N Ù GD ¹ Æ). Các trạng thái trong GD được mô tả theo một trong hai đặc tính:
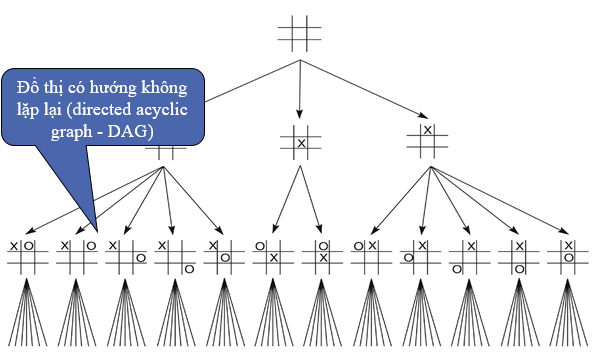
  • Đặc tính có thể đo lường được các trạng thái gặp trong quá trình tìm kiếm. VD: Tic-tac-toe, 8-puzzle,…
  • Đặc tính của đường đi được hình thành trong quá trình tìm kiếm. VD: TSP
• Đường đi của lời giải (solution path) là một con đường đi qua đồ thị này từ một nút thuộc S đến một nút thuộc GD.

Một phần KGTT triển khai trong Tic-tac-toe

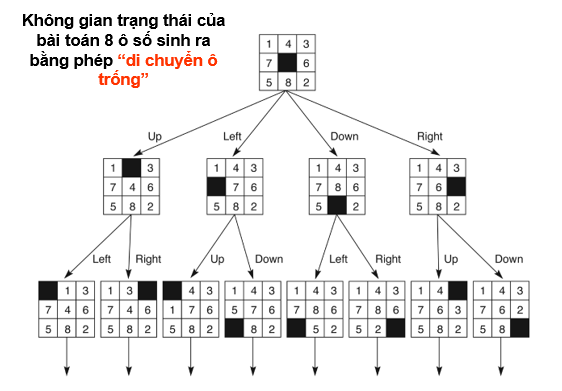
Trò đố 8 ô hay 15 ô

Trạng thái ban đầu                                                     Trạng thái đích

• Trò đố 15 ô

                   

 

• Trò đố 8 ô

                                                             

Cần biểu diễn KGTT cho bài toán này như thế nào?

Biểu diễn không gian trạng thái bài toán người đưa thư

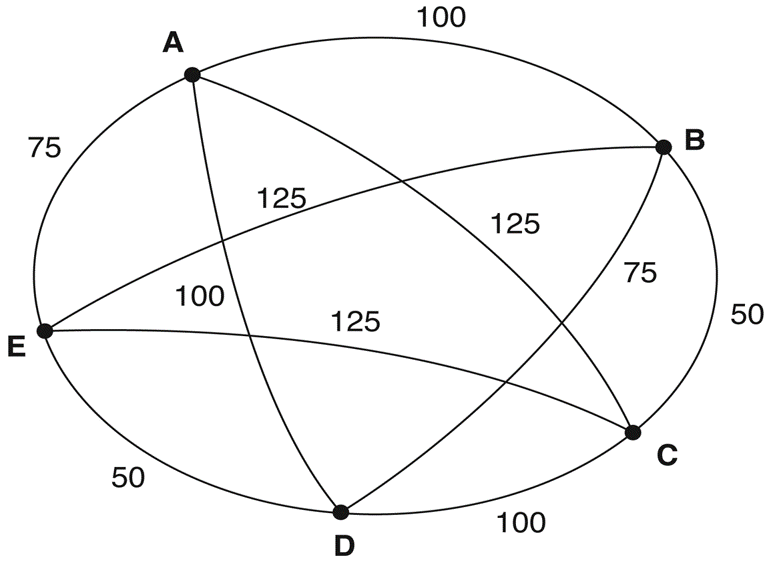
• Cần biểu diễn KGTT cho bài toán này như thế nào?

 

Các yếu tố xác định không gian trạng thái

1. 1. Trạng thái.
   2. Hành động.
   3. Kiểm tra trạng thái thoả đích.
   4. Chi phí cho mỗi bước chuyển trạng thái.

3. Phân loại vấn đề

Các đặc trưng của vấn đề

1. Không gian bài toán có đoán định được trước? (sau mỗi bước giải).
2. Cần lời giải tốt hay tối ưu?
3. Vai trò của tri thức?
4. Quá trình giải có cần tương tác người máy?

Đơn định/nắm toán bộ không gian trạng thái

Đơn định/nắm được bộ phận trong không gian trạng thái

Không đơn định/nắm được một bộ phận của không gian trạng thái

Không đơn định/không nắm được bộ phận của không gian trạng thái

4. Các chiến lược cho TK-KGTT

TK hướng từ dữ liệu (Data-driven Search)

• Việc tìm kiếm đi từ dữ liệu đến mục tiêu

• Thích hợp khi:
  • Tất cả hoặc một phần dữ liệu được cho từ đầu.
  • Rất khó đưa ra một mục tiêu hoặc giả thuyết ngay lúc đầu.

TK hướng từ mục tiêu (Goal-driven Search)

• Việc tìm kiếm đi từ mục tiêu trở về dữ liệu.

• Thích hợp khi:
  • Có thể đưa ra mục tiêu hoặc giả thuyết ngay lúc đầu.
  • Các dữ liệu của bài toán không được cho trước, nhưng hệ thống phải đạt được trong quá trình tìm kiếm.

5. Chiến lược tìm kiếm trên đồ thị KGTT

Phương pháp đánh giá chiến lược tìm kiếm trên đồ thị KGTT:

• Chiến lược tìm kiếm là chiến lược lựa chọn thứ tự xét các nodes tạo ra.
• Các tiêu chuẩn để đánh giá chiến lược :
  • • đủ : Liệu có tìm được lời giải (nếu có)?
    • độ phức tạp thời gian: số lượng node phải xét.
    • độ phức tạp lưu trữ: Tổng dung lượng bộ nhớ phải lưu trữ (các nodes trong quá trình tìm kiếm.
    • tối ưu: Có luôn cho lời giải tối ưu.
• Độ phức tạp thời gian và lưu trữ của bài toán có thể được đo bằng:
  • • b: Độ phân nhánh của cây
    • d: Độ sâu của lời giải ngắn nhất
    • m: Độ sâu tối đa của không gian trạng thái (có thể vô hạn).

Các chiến lược tìm kiếm mù (weak/uninformed/blind search)

• Những chiến thuật tìm kiếm chỉ sử dụng thông tin từ định nghĩa của bài toán:
  1. Tìm kiếm theo chiều rộng
  2. Tìm kiếm đều giá (uniform-cost search).
  3. Tìm kiếm theo chiều sâu.
  4. Tìm kiếm theo chiều sâu có hạn
  5. Tìm kiếm sâu dần.

5.1. Tìm kiếm theo chiều rộng

• Tìm kiếm theo từng tầng. Phát triển các node gần nút nhất.
• Cài đặt:
  • L (danh sách các node đã được sinh ra và chờ được duyệt) được cài đặt dưới dạng danh sách FIFO, i.e., Các node con được sinh ra (bởi EXPAND) sẽ được đặt ở dưới cùng của L.

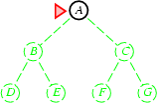
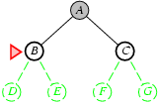
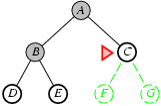
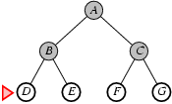
Cài đặt thuật toán tìm kiếm theo chiều rộng

Thuật toán tìm kiếm theo bề rộng được mô tả bởi thủ tục sau:

procedure Breadth_First_Search;

begin

1. Khởi tạo danh sách L chỉ chứa trạng thái ban đầu;

2. loop do

            2.1 if L rỗng then {thông báo tìm kiếm thất bại; stop};

            2.2 Loại trạng thái u ở đầu danh sách L;

            2.3 if u là trạng thái kết thúc then {thông báo tìm kiếm thành công; stop};

            2.4 for mỗi trạng thái v kề u do {

                        Đặt v vào cuối danh sách L;

                        father(v) ← u}

end;

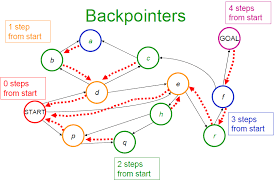
Trong thuật toán, sử dụng hàm father(v) để lưu lại cha của mỗi đỉnh trên đường đi, father(v)=u nếu u là cha của đỉnh v.

Nhận xét về thuật toán tìm kiếm theo chiều rộng.

• Trong thuật toán tìm kiếm theo chiều rộng, trạng thái nào được sinh ra trước sẽ được phát triển trước, do đó danh sách L được sử dụng là hàng đợi. Trong bước 2.3, ta cần kiểm tra xem u có là trạng thái kết thúc không. Nói chung, các trạng thái kết thúc được xác đinh bởi điều kiện nào đó.
• Nếu bài toán có nghiệm (tồn tại đường đi từ trạng thái đầu tới trạng thái kết thúc), thì thuật toán sẽ  tìm được nghiệm.

5.2. Tìm kiếm theo chiều sâu

• Phát triển các node chưa xét ở sâu nhất.
• Cài đặt:
  • L = danh sách kiểu LIFO, i.e., Đẩy các nodes con sinh bởi quá trình phát triển vào đầu L.

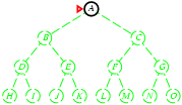
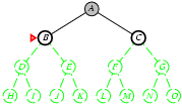
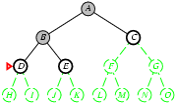
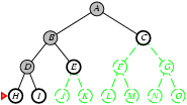
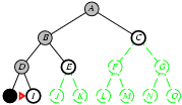
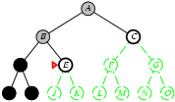
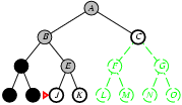
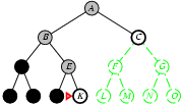
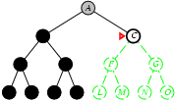
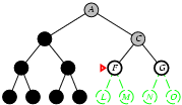
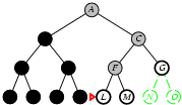
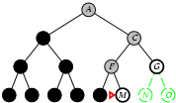
Cài đặt thuật toán tìm kiếm theo chiều sâu

Procedure Depth_First_Search;

begin

1. Khởi tạo danh sách L chỉ chứa trạng thái ban đầu u0;

2. loop do

            2.1. if L rỗng then

                        {thông báo thất bại; stop};

            2.2. Loại trạng thái u ở đầu danh sách L;

            2.3. if u là trạng thái kết thúc then

                        {thông báo thành công; stop};

            2.4. for mỗi trạng thái v kề u do

                        {Đặt v vào đầu danh sách L;};

end;

5.3. Tìm kiếm với độ sâu giới hạn

Procedure Depth_Limited_Search(d);

begin

1. Khởi tạo danh sách L chỉ chứa trạng thái ban đầu u0;

             depth(u₀) ← 0;

2. loop do

            2.1. if L rỗng then

                        {thông báo thất bại; stop};

            2.2. Loại trạng thái u ở đầu danh sách L;

            2.3. if u là trạng thái kết thúc then

                        {thông báo thành công; stop};

            2.4. if depth(u) <= d then

                        for mỗi trạng thái v kề u do

                                    {Đặt v vào đầu danh sách L;

                                    depth(v) ← depth(u) + 1};

end;

5.4. Tìm kiếm sâu dần

• Độ sâu giới hạn (depth bound):
  • Giải thuật TK sâu sẽ quay lui khi trạng thái đang xét đạt đến độ sâu giới hạn đã định.
• TK Sâu bằng cách đào sâu nhiều lần:
  • TK sâu với độ sâu giới hạn là 1, nếu thất bại, nó sẽ lặp lại giải thuật TK sâu với độ sâu là 2,…
  • Giải thuật tiếp tục cho đến khi tìm được mục tiêu, mỗi lần lặp lại tăng độ sâu lên 1.
• Giải thuật này có độ phức tạp về thời gian cùng bậc với tìm kiếm theo chiều rộng và tìm kiếm theo chiều sâu.

Tìm kiếm sâu dần d =0, 1, 2, 3

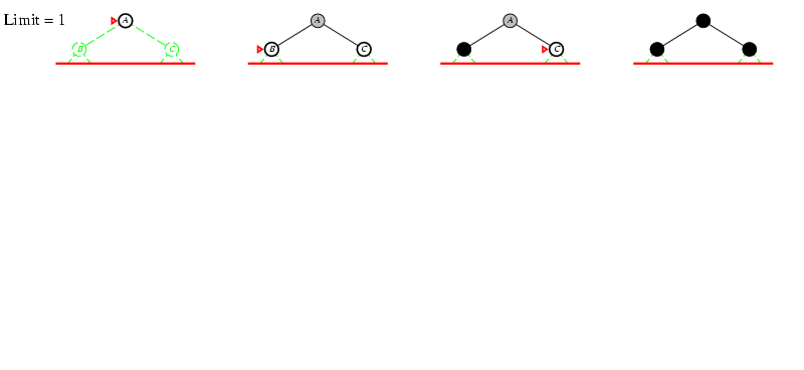
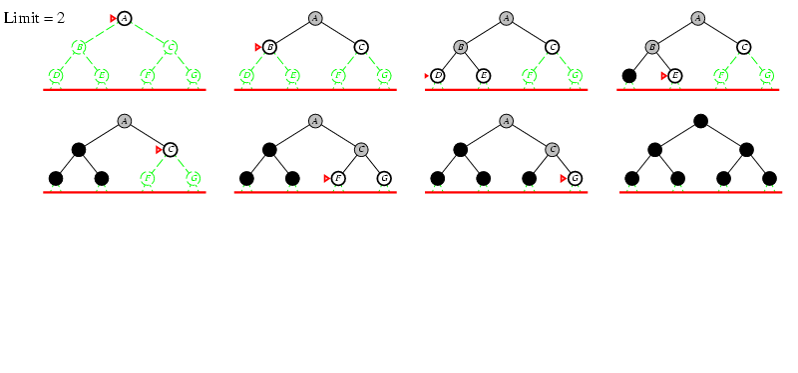
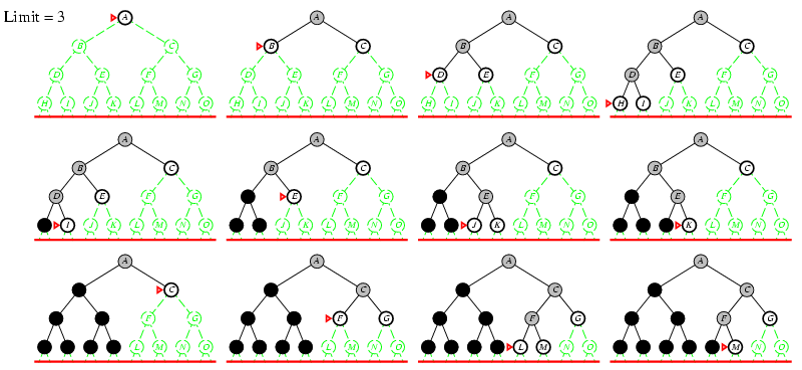
Ví dụ trò chơi ô đố 8-puzzle

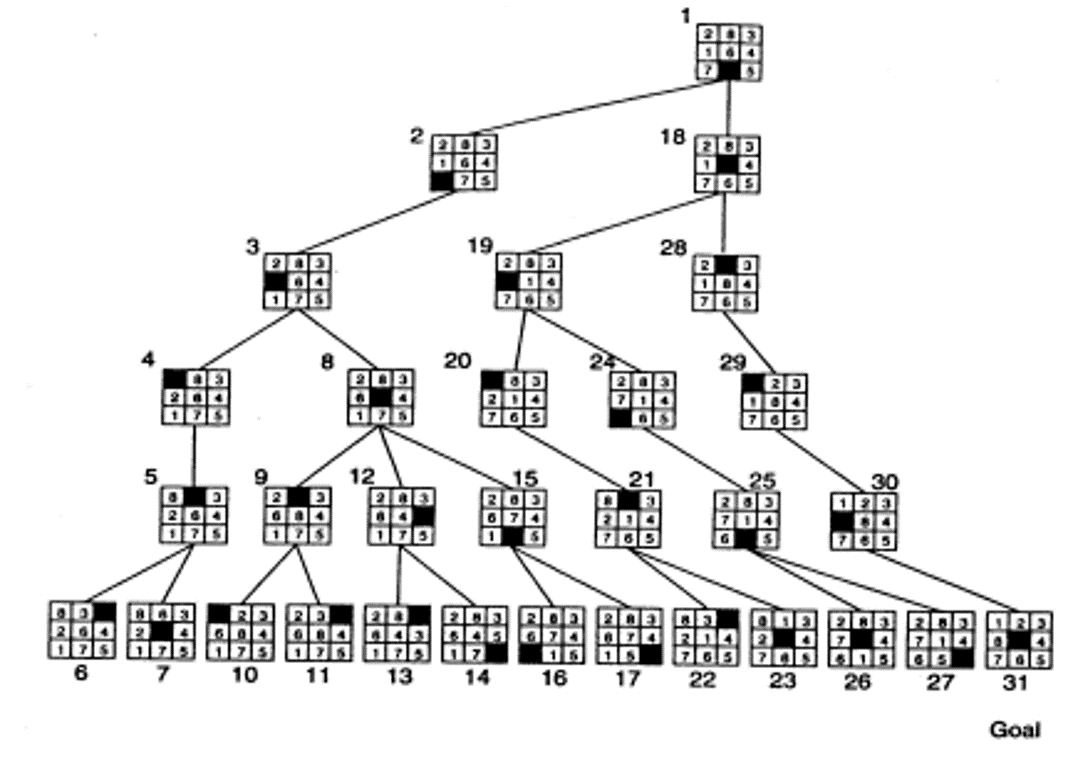
Cài đặt thuật toán tìm kiếm sâu dần

Procedure Depth_Deepening_Search;

Begin

            For d← 0 to max do

            {Depth_Limited_Search(d);

            If thành công then exit}

End;

Nhận xét về tìm kiếm sâu dần:

• Số lượng nodes được sinh trong giới hạn độ sâu d với độ phân nhánh b:

            N_DLS = b⁰ + b¹ + b² + … + b^d-2 + b^d-1 + b^d

• Số lượng nodes được sinh trong tìm kiếm sâu dần với độ sâu d độ phân nhánh b:

N_IDS = (d+1)b⁰ + d b¹ + (d-1)b² + … + 3b^d-2 +2b^d-1 + 1b^d

• Ví dụ b = 10, d = 5,.
  • N_DLS = 1 + 10 + 100 + 1,000 + 10,000 + 100,000 = 111,111.
  • N_IDS = 6 + 50 + 400 + 3,000 + 20,000 + 100,000 = 123,456.
• Tỷ lệ (123,456 - 111,111)/111,111 = 11%

Đánh giá tìm kiếm sâu dần

• • Tính đủ ?
    • Có.
  • Thời gian?
    • (d+1)b⁰ + d b¹ + (d-1)b² + … + b^d = O(b^d).
  • Không gian trạng thái?
    • O(bd).
  • Tính tối ưu?
    • Có, nếu giá mỗi bước = 1.

5.5. Chia để trị

• Thông thường, các bài toán được quy về việc tìm đường trong không gian trạng thái.
• Để giải quyết vấn đề, có thể chia nhỏ bài toán thành các vấn đề con. Việc này được thực hiện lặp lại nhiều lần đến khi các vấn đề này có thể giải quyết được.
• Một số ví dụ về phương pháp chia để trị.

Ví dụ về phương pháp: Tính tích phân

• • • Tính tích phân:
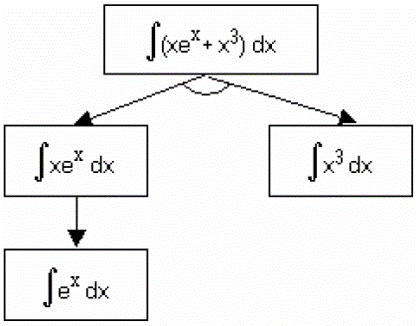
    • Để tính được tích phân này có thể sử dụng mô hình sau

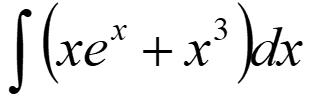
        Ví dụ về phương pháp: Tìm đường

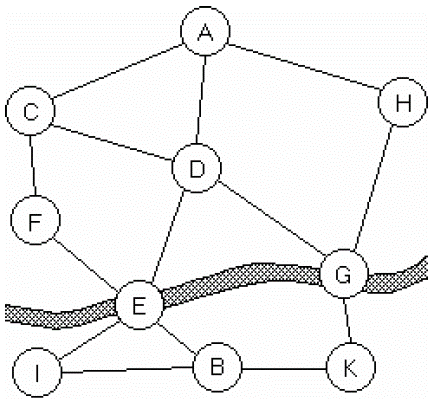
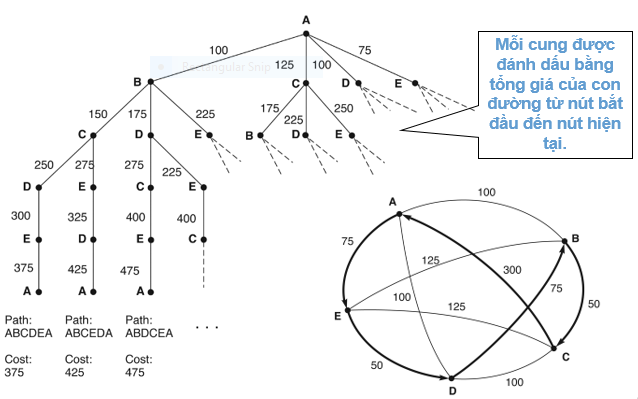
• Giả sử có bản đồ một thành phố như sau:
• Cần tìm đường đi từ A đến B. Như vậy, có thể có 2 trường hợp:
  • Đường đi từ A đến B qua E,
  • Đường đi từ A đến B qua G.
• Như vậy, bài toán tìm đường từ A đến B qua E có thể quy về các bài toán con:
  • Tìm đường từ A đến E (và),
  • Tìm đường từ E đến B.
• Bài toán tìm đường từ A đến B qua G có thể quy về các bài toán con:
  • Tìm đường từ A đến G (và),
  • Tìm đường từ G đến B.
• Các quá trình trên được minh họa bằng đồ thị (đồ thị và/hoặc) để giải quyết bài toán.

5.6. Tóm tắt chương 2

• Để giải quyết vấn đề cần phân tích các đặc trưng và yêu cầu của vấn đề.
• Việc biểu diễn dùng không gian trạng thái giúp biến quá trình giải quyết vấn đề thành một quá trình tìm kiếm (trên không gian trạng thái).
• Các chiến lược tìm kiếm khác nhau: chiều rộng, đều giá, chiều sâu, sâu dần.
• Tìm kiếm sâu dần có độ phực tạp không gian tuyến tính và độ phức tạp thời gian không quá kém so với tìm kiếm chiều rộng, chiều sâu.