1. Giới thiệu chung

• Các kỹ thuật tìm kiếm mù rất kém hiệu quả, trong nhiều trường hợp không sử dụng được.
• Trong chương này, nghiên cứu:

• Các phương pháp tìm kiếm kinh nghiệm (tìm kiếm heuristic).
• Các phương pháp sử dụng hàm đánh giá.

2. Hàm đánh giá trong tìm kiếm kinh nghiệm

• Trong tìm kiếm sử dụng kinh nghiệm, với mỗi trạng thái u, xác định một hàm h(u), hàm đánh giá, hàm này được dùng để đánh giá trạng thái “tốt”, sao cho hy vọng sẽ tới đích tốt nhất.
• Các kỹ thuật này được gọi chung là tìm kiếm kinh nghiệm (heuristic search).
• Các giai đoạn cơ bản của tìm kiếm kinh nghiệm:
  • Tìm biểu diễn thích hợp mô tả các trạng thái và các toán tử.
  • Xây dựng hàm đánh giá,
  • Thiết kế chiến lược chọn trạng thái để phát triển ở mỗi bước.

2.1. Hàm đánh giá

• Trong tìm kiếm có kinh nghiệm, hàm đánh giá đóng vai trò quan trọng.
• Nếu xây dựng hàm đánh giá đúng bản chất vấn đề → tìm kiếm có hiệu quả,
• Ngược lại, xây dựng không tốt có thể đi lệch hướng và tìm kiếm kém hiệu quả.
• Việc xây dựng hàm đánh giá tùy thuộc vào vấn đề cần giải quyết.

2.2. Một số ví dụ về hàm đánh giá

Ví dụ 1:

Trong bài toán tìm kiếm đường đi trên bản đồ, có thể xây dựng hàm đánh giá:

• • Đường chim bay từ thành phố này sang thành phố khác, hoặc
  • Sử dụng khoảng cách thực trên đường đi giữa các thành phố, hoặc
  • Sử dụng cả khoảng cách và một số trọng số khác ảnh hưởng tới việc tìm kiếm (đóng vai trò làm tăng thời gian di chuyển giữa các thành phố),
  • …..

Ví dụ 2:

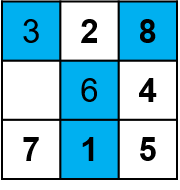
Xét bài toán 8 số, ta có thể xây dựng hàm đánh giá như sau:

Hàm H₁:

            - với một trạng thái u, H₁(u) là số quân ở sai vị trí.

            - trong ví dụ trên: H₁(u) = 4

Hàm H₂:

            - H₂(u) là tổng khoảng cách giữa vị trí quân ở trạng thái u với vị trí ở trạng thái đích.

            - trong ví dụ trên: H₂(u) = 9

3. Tìm kiếm tốt nhất đầu tiên (Best-first search)

• Ý tưởng:

Tìm kiếm tốt nhất đầu tiên = Tìm kiếm theo chiều rộng + Hàm đánh giá.

• Ý nghĩa: khác với phương pháp tìm kiếm theo chiều rộng, các node không được phát triển lần lượt mà được lựa chọn dựa trên hàm đánh giá (tốt nhất), đỉnh này có thể ở mức hiện tại hoặc ở mức trên.
• Cài đặt: Dùng hàng đợi ưu tiên. Sắp xếp các node trong hàng theo thứ tự giảm dần của hàm đánh giá.
• Một số dạng mở rộng:
  • Tìm kiếm tham lam tốt nhất đầu tiên (Greedy best-first search).
  • Tìm kiếm A* (A^* search).

3.1. Ví dụ về Best First Search

Đầu vào:

            - Trạng thái đầu là A;

            - Trạng thái kết thúc là B.

Thực hiện:

• A được xét → C, D, E.
• Chọn D, vì h(D) = 6 (min), sinh ra F,I.
• Trong số các đỉnh chưa xét C,E,F,I; chọn E vì h(E) = 7; sinh ra G và K.
• Chọn G để phát triển; sinh ra B và H.
• B là trạng thái kết thúc.

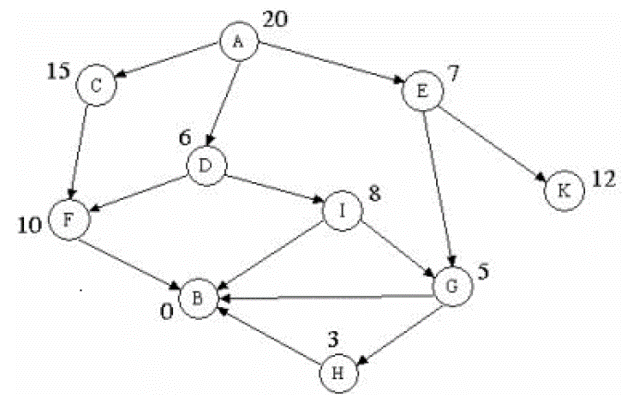
Xét không gian trạng thái sau:

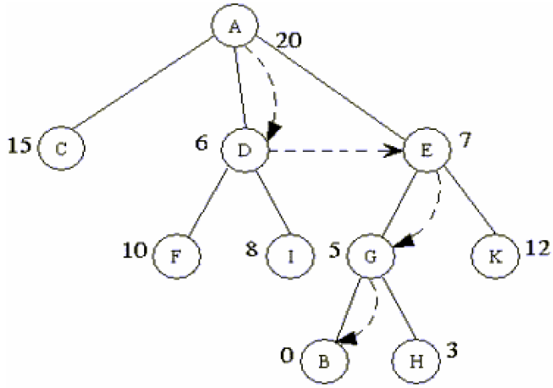
3.2. Cài đặt Best First Search

Procedure Best_First_Search;

Begin

1. Khởi tạo danh sách L chỉ chứa trạng thái ban đầu;
2. Loop do
   1. If L rỗng then { thông báo thất bại; stop; }
   2. Loại trạng thái u ở đầu danh sách L;
   3. If u là trạng thái kết thúc then  { thông báo thành công; stop; }
   4. For mỗi trạng thái v kề u do

Xen v vào danh sách L sao cho L được sắp theo thứ tự  tăng dần của hàm đánh giá;

3. End;

4. Tìm kiếm tham lam tốt nhất đầu tiên (Greedy best-first search)

• Ý tưởng:
  5. Sử dụng hàm đánh giá f(n) = h(n) (heuristic);
  6. Hàm f(n): ước lượng giá đến trạng thái đích.
• Ý nghĩa:
  5. Khác với phương pháp tìm kiếm tốt nhất đầu tiên, phương pháp này sử dụng hàm đánh giá đến trạng thái đích.
• Ví dụ:
  5. Trong tìm kiếm trên bản đồ, hàm h(n) = Khoảng cách theo đường chim bay từ n to thành phố đích.
• Nhận xét:
  5. GBFS chọn node “được cho là” gần với node đích để phát triển.

4.1. Tìm đường đi với giá tính theo km

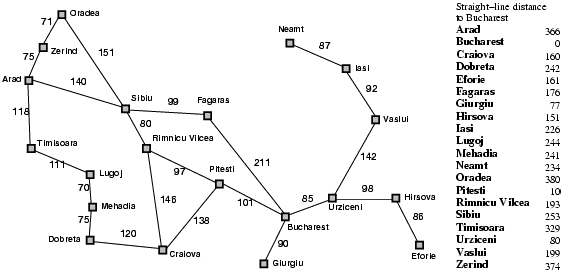
4.2. Ví dụ về GBFS

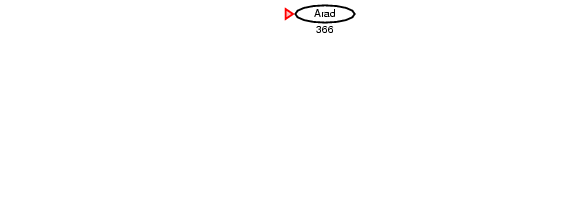
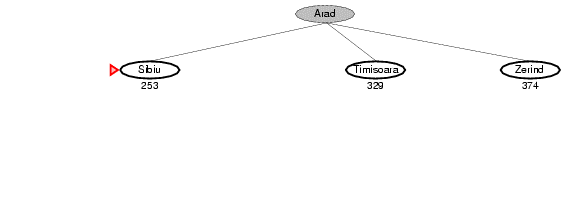
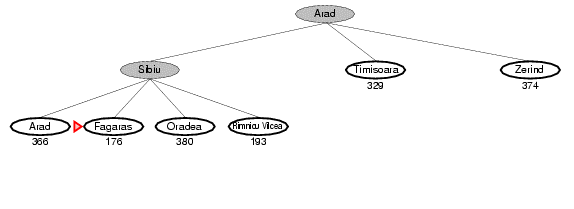
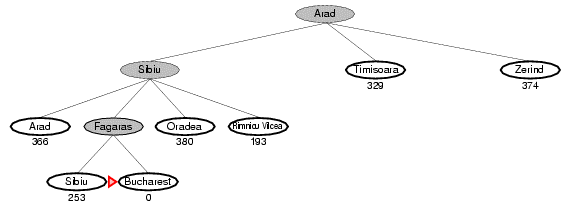
5. Tìm kiếm leo đồi (hill-climbring search)

• Ý tưởng:

Tìm kiếm leo đồi = tìm kiếm theo chiều sâu + hàm đánh giá

• Ý nghĩa:
  5. Phương pháp này được thực hiện nhờ hàm đánh giá.
  6. Khác với phương pháp tìm kiếm theo chiều sâu, khi phát triển đỉnh u, chọn trong số các đỉnh con của u, đỉnh nào có nhiều hứa hẹn nhất thì phát triển.
• Cài đặt:
  5. Sử dụng ngăn xếp có ưu tiên.

5.1. Ví dụ về Hill-climbing search

Đầu vào:

5. Trạng thái đầu là A,
6. Trạng thái kết thúc là B.

Thực hiện:

5. A được xét → C, D, E.
6. Chọn D, vì h(D) = 6 (min), sinh ra F,I.
7. Trong số các đỉnh  con của D, chọn I, vì h(I) = 8.
8. Với I được chọn, sinh ra B và G.
9. B là trạng thái kết thúc.

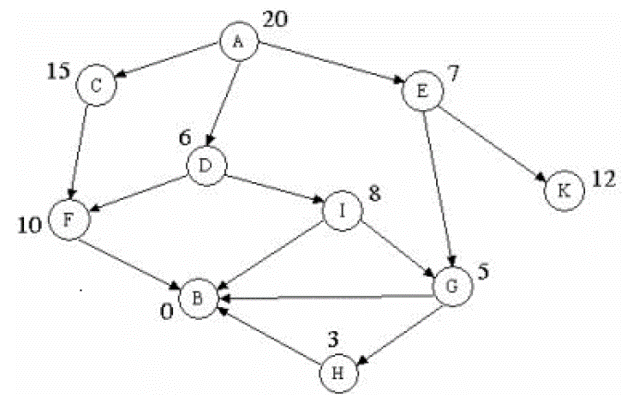
Xét không gian trạng thái sau:

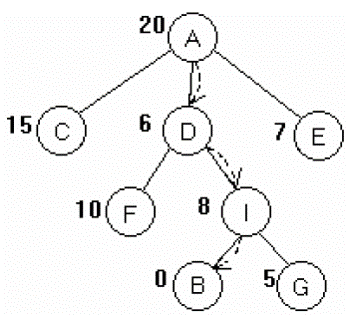
5.2. Cài đặt Hill-Climbing Search

Procedure Hill_Climbing_Search;

Begin

1. Khởi tạo danh sách L chỉ chứa trạng thái đầu;
2. Loop do
   1. If L rỗng then { thông báo thất bại; stop; }
   2. Loại trạng thái u đầu danh sách L;
   3. If u là trạng thái kết thúc then { thông báo thành công; stop; }
   4. For mỗi trạng thái v kề u đặt v vào L sao cho các phần tử được đưa vào đầu danh sách L có đánh giá giảm dần;
3. End;

6. Tìm kiếm chùm (Beam search)

• Ý tưởng:

Tìm kiếm theo chiều rộng + k node để phát triển + hàm đánh giá

• Ý nghĩa:
  5.  Tìm kiếm beam giống tìm kiếm theo chiều rộng,
  6.  Tuy nhiên trong tìm kiếm beam, hạn chế k đỉnh tốt nhất để phát triển.
  7. Như vậy, số đỉnh cần phát triển ở mức d là k^d.

6.1. Ví dụ về Beam Search

Đầu vào:

5. Trạng thái đầu là A,
6. Trạng thái kết thúc là B.

Thực hiện:

• Ví dụ lấy k = 2.
• A được xét → C, D, E.
• Chọn D và E để phát triển, với D sinh ra F và I, với E sinh ra G và K.
• Chọn I và G để phát triển, sinh ra B, G, B, H
• Chọn được B (qua I) và B (qua G).
• B là trạng thái kết thúc.

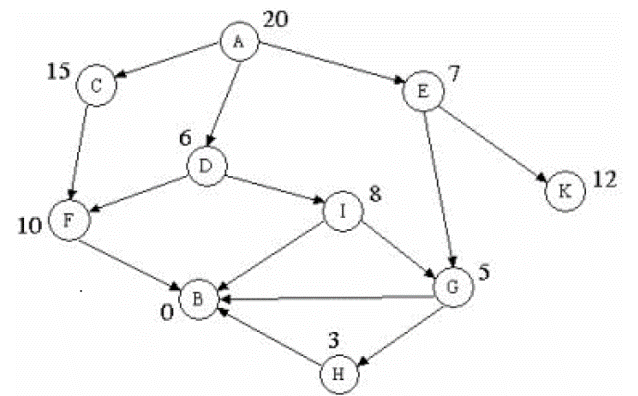
Xét không gian trạng thái sau:

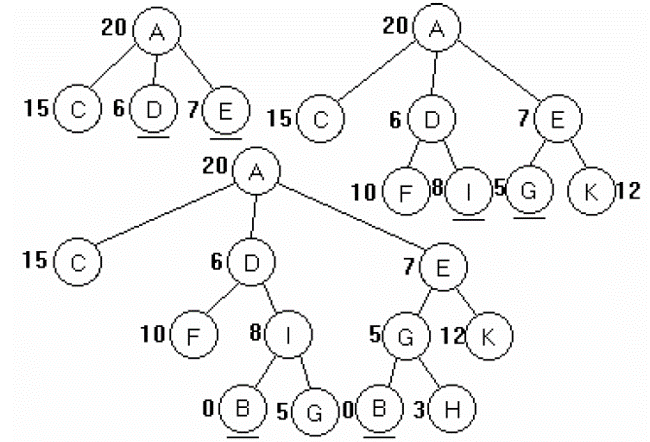
7. Heuristic chấp nhận được

Trong kỹ thuật tìm kiếm, để việc tìm kiếm có hiệu quả sẽ sử dụng hàm đánh giá để hướng dẫn tìm kiếm. Các kỹ thuật này thuộc nhóm tìm kiếm Heuristic.

• Giả sử u là một trạng thái đạt tới (có đường đi từ trạng thái đầu u₀ tới u); hàm đánh giá được xác định như sau:
  • g(u): đánh giá độ dài đường đi ngắn nhất từ u₀ tới u.
  • h(u): đánh giá độ dài đường đi ngắn nhất từ u tới trạng thái đích.

Hàm h(u) được gọi là chấp nhận được nếu với mọi trạng thái u, thì

h(u) ≤ độ dài đường đi ngắn nhất thực tế từ u tới trạng thái đích.

• • Để tăng hiệu quả của quá trình tìm kiếm:

f(u) = g(u) + h(u)

7.1. Heuristics chấp nhận được trong A*

• Hàm heuristic h(u) là chấp nhận được nếu với mọi node u, h(u) ≤ h^*(u),
  5. Trong đó h^*(u) là chi phí  thực để đi đến đích từ u.
• Ý nghĩa:
  5. Heuristic chấp nhận được không bao giờ đánh giá chi phí cao quá thực tế.
• Ví dụ: h_SLD(u) là Heuristic chấp nhận được.
• Định lý:
  5. Nếu h(n) là chấp nhận được, A^* là thuật toán cho lời giải tối ưu.

7.2. So Sánh các Heuristics

• Nếu h₂(u) ≥ h₁(u) với mọi u (cả hai đều chấp nhận được)
  5. thì h₂ được coi là mạnh hơn h₁
  6. h₂ là heuristic tốt hơn
• Ví dụ tìm kiếm trên bài toán 8-số (số lượng node trung bình phải xét):
  5. d=12   IDS = 3,644,035 nodes
                             A^*(h₁) = 227 nodes
                             A^*(h₂) = 73 nodes
  6. d=24   IDS = too many nodes
                             A^*(h₁) = 39,135 nodes
                             A^*(h₂) = 1,641 nodes

8. A^* search

• Ý tưởng:
  5.  Sử dụng hàm Heuristics chấp nhận được + tìm kiếm theo chiều rộng → Loại bỏ những đường đi có chi phí cao.
• Hàm lượng giá: f(u) = g(u) + h(u)
  5.  g(u) = Chi phí để đến u
  6.  h(u) = Lượng giá từ u đến đích
  7.  f(u) = Ước lượng tổng giá đến đích qua u.

8.1. Tìm đường đi với giá tính theo km

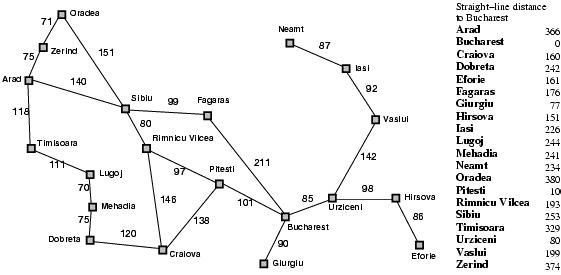
8.2. Ví dụ về A^* search

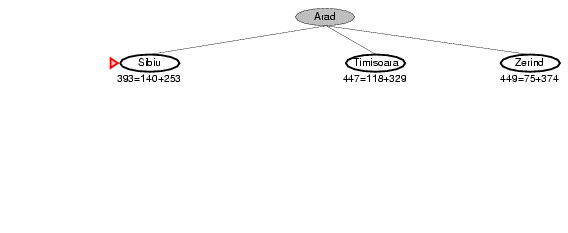
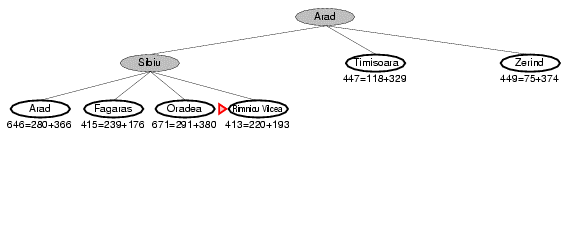
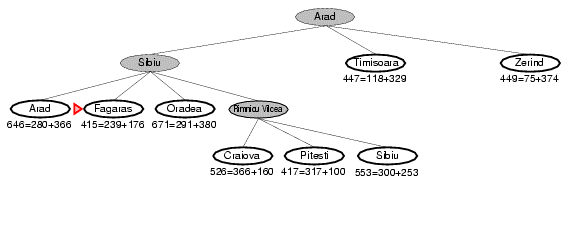
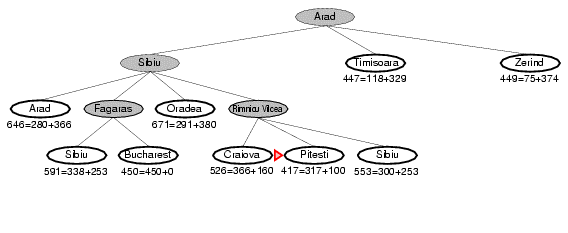
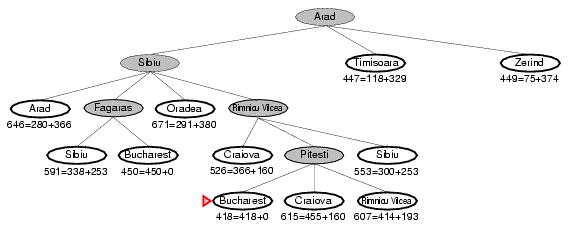
8.2. Ví dụ về A^* search (ví dụ 2)

Đầu vào:

§Trạng thái đầu A,

§Trạng thái đích B.

§Các giá trị ghi trên cạnh là độ dài đường đi;

§Các số cạnh các đỉnh là giá trị hàm h.

Yêu cầu:

—Tìm đường đi ngắn nhất từ A đến B bằng A*.

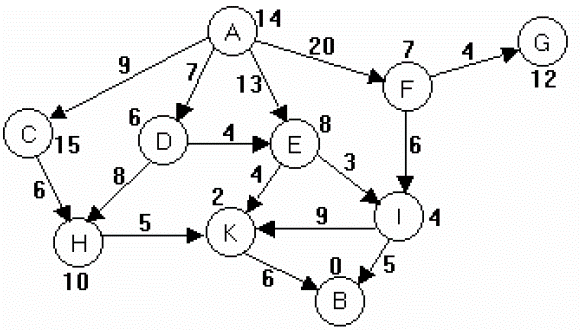
Không gian trạng thái với hàm đánh giá

Thực hiện:

v Phát triển đỉnh A sinh ra các đỉnh con C, D, E, F.

v g(C) = 9, h(C) = 15    →   f(C) = 9 + 15 = 24

v g(D) = 7, h(D) = 6     →   f(D) = 7 + 6 = 13

v g(E) = 13, h(E) = 8   →   f(E) = 13 + 8 = 21

v g(F) = 20, h(F) = 7   →   f(F) = 20 + 7 = 27

  → Như vậy, đỉnh D được chọn để phát triển (f(D) = 13)

 

—Phát triển D, nhận được các đỉnh con H và E (mới). Trong đó:

Øg(H) = g(D) + độ dài cung (D,H) = 7 + 8 = 15

Øh(H) = 10

Ø→ f(H) = g(H) + h(H) = 15 + 10 = 25.

Ø

Øg(E) = g(D) + độ dài cung (D,E) = 7 +4 = 11

Øh(E) = 8

→ f(E) = g(E) + h(E) = 11 + 8 = 19.

—Như vậy đỉnh E sẽ được dùng để phát triển tiếp

—Tương tự sẽ chọn được các đỉnh K, B (đích).

—Với g(B) = 19, h(B) = 0.

—Đường đi: A → D → E → I →B

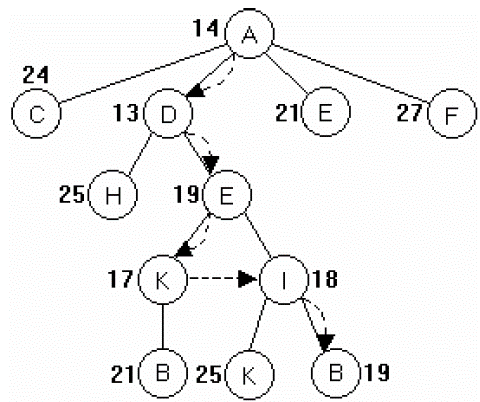
8.3. Cài đặt thuật toán A*

Procedure A*;

Begin

1.Khởi tạo danh sách L chỉ chứa trạng thái đầu.

2.Loop do

2.1. if L rỗng then {thông báo thất bại; stop;}

2.2. Loại trạng thái u ở đầu danh sách L;

2.3. if u là trạng thái đích then {thông báo thành công; stop}

2.4. for mỗi trạng thái v kề u do

  {   g(v) ← g(u)+ k(u,v); 

  f(v) ← g(v)+h(v);

  Đặt v vào danh sách L;    }

2.5. Sắp xếp L theo thứ tự giảm dần của hàm f sao cho trạng thái có giá trị của hàm f nhỏ nhất ở đầu danh sách;

3. End;