Cây trò chơi và tìm kiếm trên cây trò chơi

• Trong bài, nghiên cứu các trò chơi có hai người tham gia; như:
  • cờ vua,
  • cờ ca rô,
  • cờ tướng...
• Người chơi là quân Trắng, đối thủ là quân Đen.
• Mục tiêu: nghiên cứu giải thuật cho quân Trắng đi.

Một số đặc điểm:

• • 2 người thay phiên đưa ra các nước đi tuân theo một luật nào đó.
  • Các luật trên là như nhau cho cả 2 người.
  • Cả 2 người chơi đều biết được thông tin đầy đủ về các tình thế trong trò chơi.
  • Trong vấn đề trò chơi, thực chất là tìm kiếm nước đi, một nước tốt sao cho, sau một số nước đi dẫn đến trạng thái kết thúc.

Khó khăn:

• Vấn đề tìm kiếm ở đây khó khăn hơn với việc tìm kiếm trong các bài trước, vì:
  • Ở trong vấn đề này, có đối thủ, nên không biết đối thủ sẽ đi như thế nào.
  • Nếu có thể tổng quát, cũng sẽ rất khó vì không gian tìm kiếm quá rộng.
  • Nói chung, không thể tìm được lời giải tối ưu, chỉ tìm được lời giải xấp xỉ.

Giải pháp: trong trò chơi, có thể coi như tìm kiếm trong không gian trạng thái, mỗi trạng thái là một tình thế của trò chơi. Có thể tóm tắt giải pháp:

• • Trạng thái ban đầu là sự sắp xếp các quân cờ trong lúc đầu của cuộc chơi.
  • Các nước đi hợp lệ là các toán tử.
  • Các trạng thái kết thúc là các tình thế mà cuộc chơi dừng, thường đã xác định, có thể thông qua hàm kết quả.
  • Có thể biểu diễn không gian trạng thái trên cây trò chơi.

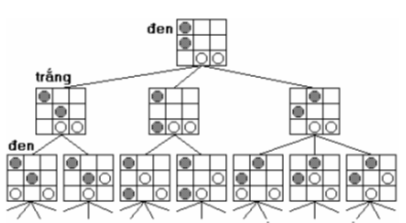
Cách xây dựng cây trò chơi:

• • Gốc của cây ứng với trạng thái u.
  • Có thể gọi đỉnh ứng với trạng thái Trắng (Đen) đưa ra nước đi là đỉnh Trắng (Đen).
  • Nếu một đỉnh là Trắng (Đen) ứng với trạng thái u, thì đỉnh con của nó là tất cả các đỉnh biểu diễn trạng thái v, v nhận được từ u do Trắng (Đen) thực hiện nước đi hợp lệ nào đó.

Nhận xét:

• • Độ cao của cây là tổng số nước đi của cả 2 người.
  • Trên cùng một mức của cây, các đỉnh đều là Trắng hoặc Đen.
  • Các lá của cây ứng với các trạng thái kết thúc.

Ví dụ: Xét trò chơi Dodgen (được đưa ra bởi Colin Vout):

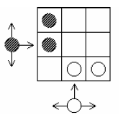
• • Trên bàn cờ có 2 loại quân Trắng và Đen, được sắp trên bàn cờ 3x3. (như hình vẽ)
  • Quân đen có thể đi tới ô trống bên phải, ở trên hoặc bên dưới.
  • Quân đen nếu ở cột ngoài cùng có thể đi ra ngoài bàn cờ.
  • Quân trắng có thể đi tới ô trống ở bên trái, bên phải, ở trên.
  • Quân trắng nếu ở hàng trên cùng có thể đi ra ngoài bàn cờ.
  • Trạng thái kết thúc: ai đưa được quân 2 quân của mình ra khỏi bàn cờ; hoặc bắt đối phương không đi được nữa.

Ví dụ: Trò chơi Dodgen.

Trạng thái đầu của trò chơi Dodgen

Cây trò chơi Dodgen với quân Đen đi trước

Ví dụ: Trò chơi dạng caro:

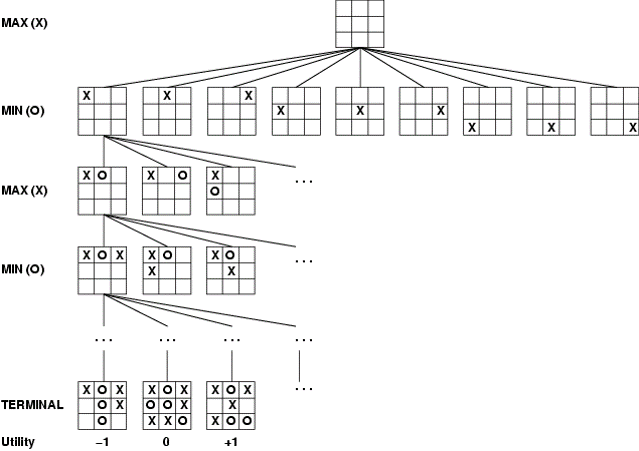
Chiến lược Minimax

Một số nhận định về chiến lược Minimax:

• • Giả sử đến một thời điểm đường đi đã dẫn tới đỉnh u.
  • Nếu u là đỉnh Trắng thì Trắng cần chọn đi tới một trong các Đen v là con của u.
  • Nước đi tối ưu cho Trắng là nước đi dẫn tới đỉnh con v là đỉnh tốt nhất cho Trắng trong số các đỉnh con. Tương tự cho việc lựa chọn nước đi cho quân Đen.
  • Để chọn nước đi tốt nhất cho Trắng tại đỉnh u, ta cần xác định giá trị các đỉnh của cây trò chơi có gốc là u.
  • Giá trị của các lá được xác định thông qua hàm kết quả.
  • Đỉnh có giá trị càng lớn càng tốt cho Trắng, đỉnh có giá trị càng nhỏ càng tốt cho Đen.

Cách tính điểm cho các đỉnh trên cây trò chơi:

• • Để xác định giá trị các đỉnh có gốc là u, ta đi từ mức thấp nhất đến u.
  • Giả sử xét đỉnh v trên cây, các giá trị các đỉnh con của nó đã xác định.
  • Nếu v là đỉnh Trắng, giá của nó được xác định là giá trị lớn nhất trong các giá trị của các đỉnh con.
  • Nếu v là đỉnh Đen, giá của nó là giá trị nhỏ nhất trong các giá trị của các đỉnh con.

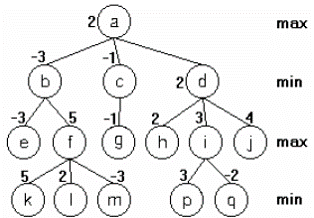
Gán giá trị cho các đỉnh của cây trò chơi.

Ví dụ:

            đỉnh f là đỉnh Trắng, giá của đỉnh f = max(5,2,-3) = 5

            đỉnh d là đỉnh Đen, giá của đỉnh d = min(2,3,4) = 2

Các hàm trong chiến lược Minimax

Hàm gán giá trị max:

Function MaxValue(u);

Begin

If u là lá then MaxValue(u) ← f(u)

Else MaxValue(u) ← max {MinValue(v) | v là các đỉnh con của u}

End;

Hàm gán giá trị min:

Function MinValue(u);

Begin

If u là lá then MinValue(u) ← f(u)

Else MinValue(u) ← min {MaxValue(v) | v là các đỉnh con của u}

End;

Thủ tục minimax:

Procedure Minimax(u,v);

Begin

Value ← - ∞;

For mỗi w là đỉnh con của u do

If Value <= MinValue(w) then

Begin Value ← MinValue(w);

           v ← w; end;

End;

Trong đoạn chương trình trên, chọn nước đi cho Trắng tại u, v là biến lưu lại trạng thái mà Trắng đa chọn đi tới từ u.

Đánh giá về chiến lược Minimax:

1. Tính đủ
   • Có (nếu cây tìm kiếm là hữu hạn).
2. Tính tối ưu
   • có (đối với đối thủ luôn ra nước tối ưu)
3. Độ phức tạp thời gian?
   • O(b^m) (với m là độ cao của cây, tại mỗi đỉnh có b nước đi)
4. Độ phức tạp không gian?
   • O(bm) (DFS)

• Ví dụ cờ vua, thông thường b ≈ 35, m ≈100  à Tìm lời giải chính xác và tối ưu là không thể được

Hàm đánh giá trong chiến lược Minimax:

• • Trong chiến lược Minimax, nếu có hàm f(), hàm kết quả, thì chương trình có giá trị tối ưu, tuy nhiên, cần xét cả không gian trạng thái của cây trò chơi.
  • Để tìm ra kết quả nhanh, nước đi tốt, ta có thể sử dụng hàm đánh giá, hàm này chỉ xét một bộ phận của cây trò chơi.
  • Chất lượng của chương trình phụ thuộc vào hàm đánh giá, nếu hàm đánh giá không chính xác về trạng thái sẽ cho nước đi kém.
  • Hàm đánh giá phụ thuộc vào nhiều nhân tố của trò chơi. Ở đây có sự mâu thuẫn giữa độ chính xác và thời gian tính toán.
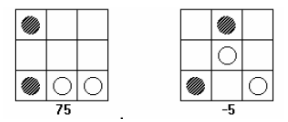
  • Trong trò chơi Dodgen, hàm đánh giá eval() xác định lợi thế của trạng thái u.
    • Nếu eval() càng dương, thuận lợi cho Trắng;
    • Nếu eval() càng âm, thuận lợi cho Đen;
    • Nếu eval() ≈ 0 thì không thuận lợi cho ai cả.

Ví dụ: Một số hàm đánh giá

Ví dụ 1: Xây dựng hàm đánh giá cho bàn cờ vua.

• • Mỗi quân trên bàn cờ được gán một giá trị, phù hợp với “sức mạnh” của con cờ. Giả sử:
    • Quân tốt Trắng (Đen) được gán giá trị 1(-1)
    • Quân mã Trắng (Đen) được gán giá trị 3(-3)
    • Quân xe Trắng (Đen) được gán giá trị 5(-5)
    • Quân hậu Trắng (Đen) được gán giá trị 9(-9)
  • Hàm đánh giá tại mỗi trạng thái:

Eval() = s₁w₁ + s₂w₂ + ... + s_nw_n.

• • Nhận xét: Hàm trên không quan tâm tới vị trí quân cờ.

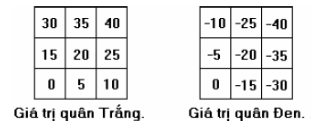
Ví dụ 2: Xây dựng hàm đánh giá cho trò chơi Dodgen.

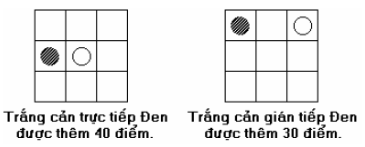
• Mỗi vị trí của quân Trắng (Đen) được cho giá trị như hình vẽ.

• Nếu quân Trắng cản trực tiếp quân Đen thì thêm 40 điểm, nếu cản gián tiếp được thêm 30 điểm.
• Ngược lại, nếu quân Đen cản trực tiếp quân Trắng thì thêm -40 điểm, nếu cản gián tiếp được thêm -30 điểm.

Xây dựng hàm đánh giá cho trò chơi Dodgen.

Nhận xét: Với cách xây dựng như trên, hàm đánh giá có xét tới vị trí các quân trên bàn cờ và mối tương quan giữa các quân cờ.

Xây dựng hàm đánh giá cho trò chơi Dodgen.

Giá trị của một số trạng thái trong Dodgen

Chiến lược minimax với độ sâu cố định

• • Trong các trò chơi, hiếm khi có khả năng mở rộng đến nút lá.
  • Khi đó, có thể áp dụng chiến lược tính trước n bước đi.
  • Giá trị trong các nút con không phản ánh giá trị thắng thua, chỉ phản ánh giá trị heuristic nào đó.
  • Giá trị được truyền ngược cũng không đánh giá việc thắng thua, cũng chỉ là giá trị heuristic của trạng thái tốt nhất có thể tiếp cận.
  • Minimax đối với một KGTT giả định.

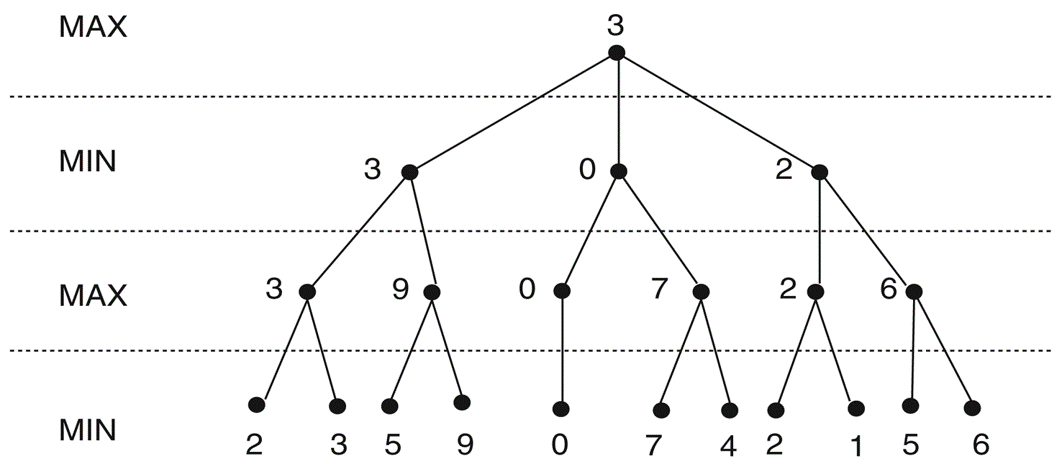
• • Các nút lá được gán các giá trị heuristic
  • Còn giá trị tại các nút trong là các giá trị nhận được dựa trên giải thuật Minimax

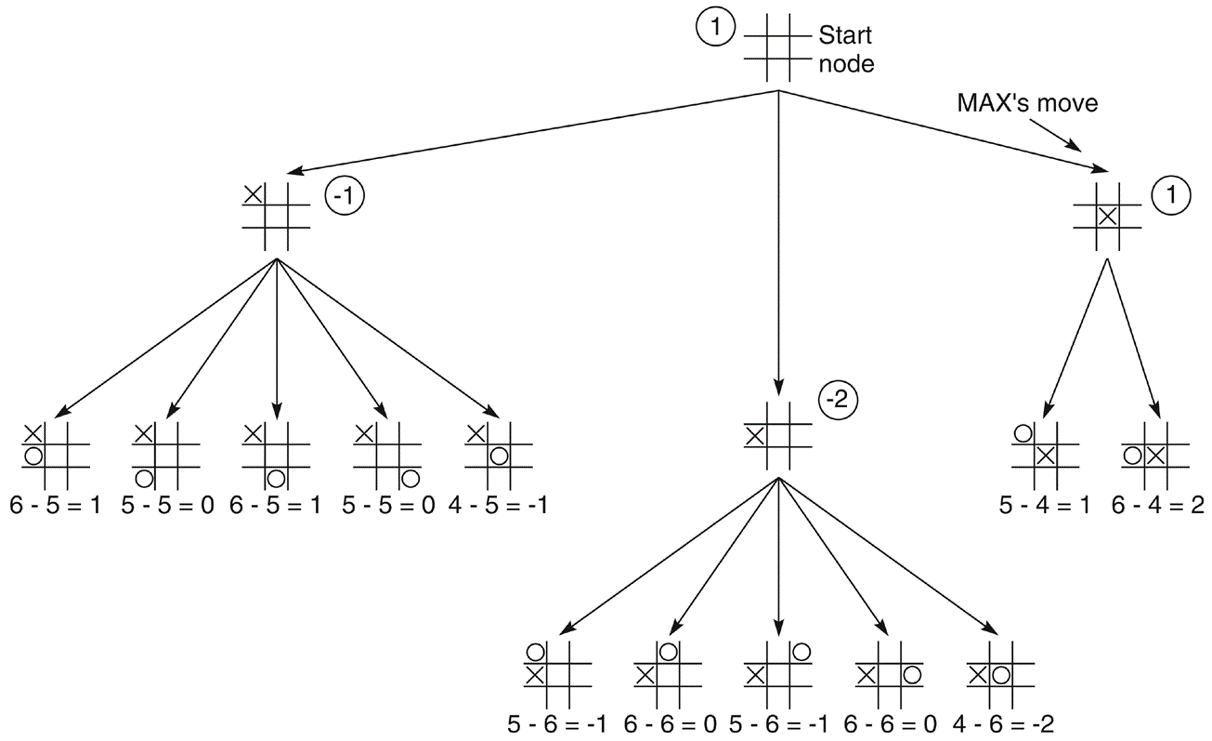
Heuristic trong trò chơi tic-tac-toe

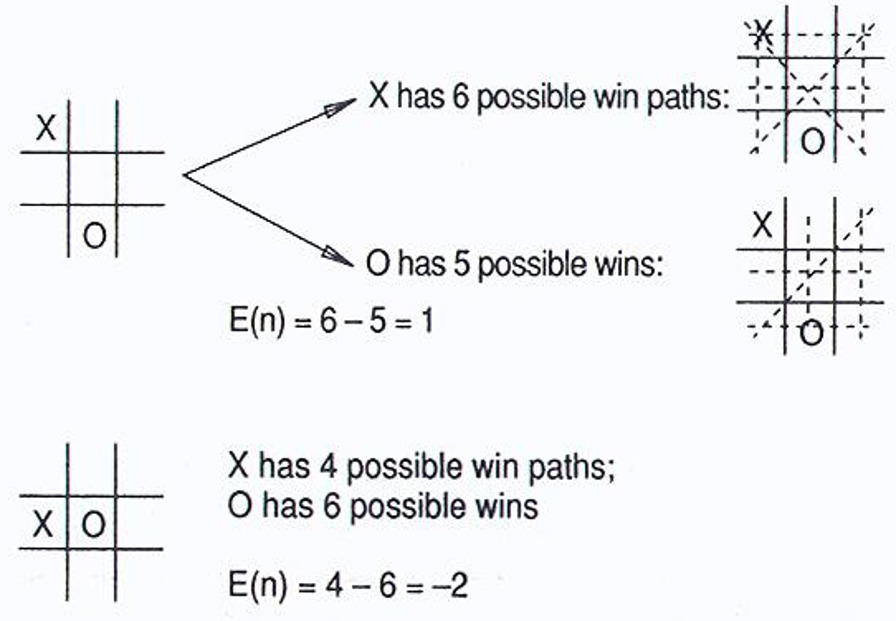
• Hàm Heuristic:          E(n) = M(n) – O(n)

    Trong đó:    M(n) là tổng số đường thắng có thể của tôi

                        O(n) là tổng số đường thắng có thể của đối thủ

                        E(n) là trị số đánh giá tổng cộng cho trạng thái n

Phương pháp cắt tỉa alpha-beta

Nhận xét về các giải thuật trước:

• • Trong chiến lược minimax, để tìm nước đi tốt cho quân Trắng tại trạng thái u, cho dù đã hạn chế không gian bằng việc giảm độ cao, thì cũng rất lớn nếu h>=3.
  • Ví dụ:
    • Với trò chơi cờ vua, nếu máy tính có thể tính 10⁶  nước/s

            b^m = 10⁶, b=35 à m=4

• • • Tuy nhiên,
      • 4-ply ≈ người mới học chơi
      • 8-ply ≈ PC, chuyên gia cờ
      • 12-ply ≈ Deep Blue, Kasparov.

Tư tưởng của phương pháp alpha-beta:

• • Giả sử quá trình tìm kiếm đi xuống đỉnh Trắng a, đỉnh a có đỉnh cùng cấp v đã xét.
  • Giả sử đỉnh a có cha là b, b có đỉnh cùng cấp là u đã xét; cha của b là c.
  • Khi đó, giá của c ít nhất là u, giá của b nhiều nhất là v.
  • Nếu eval(u)> eval(v), ta không cần đi xuống đỉnh a nữa mà không ảnh hưởng tới giá của c.
  • Lập luận tương tự cho đỉnh a là Đen, với đánh giá eval(u)<eval(v).

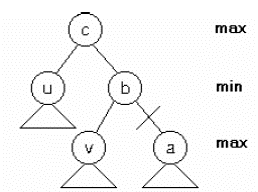
Cắt tỉa gốc a nếu eval(u)>eval(v)

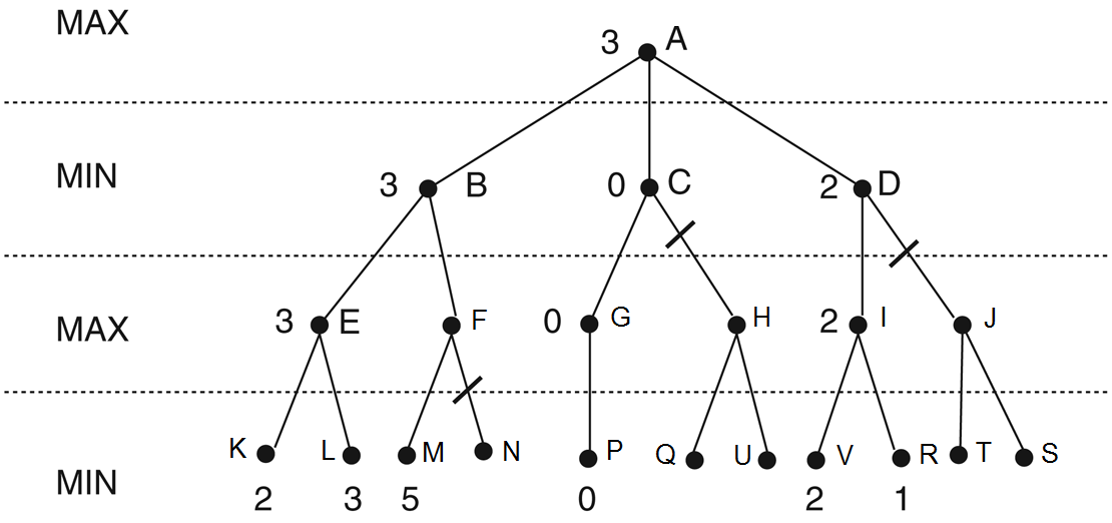
• Xét K(2) và L(3), khi đó E có giá trị 3 = max(2,3).
• Vì M=5, nên ít nhất F=5, do đó, không cần xét nhánh N, có thể kết luận B=3 (cắt bỏ beta).
• Tương tự, xét P(0), suy ra G=0. Do chọn min, suy ra C nhiều nhất =0. Vì A chọn max, nên không cần xét H.
• Tương tự, D nhiều nhất bằng 2, mà chọn A theo max, B>I, nên không cần xét J.

Các hàm trong chiến lược Alpha-beta

• Hàm sử dụng α để ghi giá trị lớn nhất trong các giá trị của đỉnh con đã đánh giá của một đỉnh trắng, β ghi giá trị nhỏ nhất trong các đỉnh con của một đỉnh đen.
• Hàm MaxValue(u, α, β) tính giá của đỉnh Trắng u.
• Hàm MinValue(u, α, β) tính giá của đỉnh Đen u.

Hàm gán giá trị max:

Function MaxValue(u, α, β);

Begin

If u là lá của cây hạn chế hoặc là đỉnh kết thúc

then MaxValue ← eval(u)

Else

            for mỗi đỉnh v là con của u do

                  begin

                         α ← max {α, MinValue(v, α, β)};

                        if α > β then exit;

                  end;

MaxValue ← α;

End;

Hàm gán giá trị min:

Function MinValue(u, α, β);

Begin

If u là lá của cây hạn chế hoặc là đỉnh kết thúc

then MinValue ← eval(u)

Else

            for mỗi đỉnh v là con của u do

                  begin

                         β ← min {β, MaxValue(v, α, β)};

                        if α > β then exit;

                  end;

MinValue ← β;

End;

Thủ tục Alpha-Beta: (tìm nước đi cho quân Trắng, v là đỉnh cần tới)

Procedure Alpha_Beta(u, v);

Begin

α ← -∞;

β ← ∞;

for mỗi đỉnh w là đỉnh con của u do

If α<=MinValue(w, α, β) then

   begin

                α=MinValue(w, α, β);

                v = w;

    end;

End;